复变函数B 习题解答 第一章

第一章：复数和平面点集

1. 计算

1. 原式 $=3^2+\sqrt{3}^2=12$
2. 原式 $\begin{aligned}=&(x-i\sqrt{y})(-x-i\sqrt{y})-i\sqrt{y}(x-i\sqrt{y})\\=&-x^2-y-ix\sqrt{y}-y\\=&-x^2-2y-ix\sqrt{y}\\[-32pt]\end{aligned}$
3. 原式 $=\frac{(3-4i)(4-3i)}{25}=\frac{12-12-25i}{25}=-i$
4. 原式 $=\frac{5i(\sqrt{2}+\sqrt{3}i)}{5}=-\sqrt{3}+\sqrt{2}i$

2. 用三角式及指数式表示下列复数，并求辐角一般值

1. $\begin{aligned}z=&2\sqrt{2}(\cos-\frac{\pi}{4}+i\sin-\frac{\pi}{4})\\=&2\sqrt{2}e^{i(-\frac{\pi}{4})}\\[-19pt]\end{aligned}$
   $Arg z=\arg z+2k\pi=2k\pi-\frac{\pi}{4}(k\in\mathbb{Z})$
2. $\begin{aligned}z=&\sqrt{3}(\cos-\frac{\pi}{2}+i\sin-\frac{\pi}{2})\\=&\sqrt{3}e^{i(-\frac{\pi}{2})}\\[-19pt]\end{aligned}$
   $Arg z=\arg z+2k\pi=2k\pi-\frac{\pi}{2}(k\in\mathbb{Z})$
3. $|z|=\frac{\sqrt{13}}{2}$
   $\arg z=-\pi+\arctan\frac{\sqrt{3}}{1/2}=-\pi+\arctan2\sqrt{3}$
   $\begin{aligned}z=&2\sqrt{2}(\cos(-\pi+\arctan2\sqrt{3})+i\sin(-\pi+\arctan2\sqrt{3}))\\=&2\sqrt{2}e^{i(-\pi+\arctan2\sqrt{3})}\\[-19pt]\end{aligned}$
   $Arg z=\arg z+2k\pi=2k\pi-\pi+\arctan2\sqrt{3}(k\in\mathbb{Z})$
4. 设 $\theta=\theta_0+2n\pi(n\in\mathbb{Z},0\le\theta_0<2\pi)$
   $\theta_0=0$ 时 $z=0$，辐角无意义
   $\theta_0\not=0$ 时，$\arg z=\arctan\frac{\sin\theta_0}{1-\cos\theta_0}=\arctan\frac{1}{\tan(\theta_0/2)}=\frac{\pi-\theta_0}{2}$
   $|z|=\sqrt{(1-\cos\theta_0)^2+\sin^2\theta_0}=2\sin\frac{\theta_0}{2}$
   $\begin{aligned}z=&2\sin\frac{\theta_0}{2}(\cos\frac{\pi-\theta_0}{2}+i\sin\frac{\pi-\theta_0}{2})\\=&2\sin\frac{\theta_0}{2}e^{i(\frac{\pi-\theta_0}{2})}\\[-19pt]\end{aligned}$
   $Arg z=\arg z+2k\pi=2k\pi+\frac{\pi-\theta_0}{2}(k\in\mathbb{Z})$

3. 利用复数三角式或指数式计算

1. 原式 $\begin{aligned}=&e^{i\cdot\frac{\pi}{2}}\cdot2e^{i(-\frac{\pi}{3})}\cdot2e^{i\cdot\frac{\pi}{6}}\\=&4e^{i\cdot\frac{\pi}{3}}\\[-19pt]\end{aligned}$
2. 原式 $\begin{aligned}=&(2e^{i\cdot\frac{\pi}{6}})^{-3}\\=&\frac{1}{8}e^{i(-\frac{\pi}{2})}=-\frac{i}{8}\\[-24pt]\end{aligned}$
3. 原式 $\begin{aligned}=&\sqrt[3]{\sqrt{2}e^{i\cdot\frac{\pi}{4}}}\\=&\sqrt[6]{2}\cdot e^{i(\frac{\pi}{12}+\frac{2\pi k}{3})}(k=0,1,2)\\[-19pt]\end{aligned}$

4. 解方程

1. 原式 $\begin{aligned}=&\sqrt[3]{2e^{i(-\frac{\pi}{3})}}\\=&\sqrt[3]{2}\cdot e^{i(-\frac{\pi}{9}+\frac{2\pi k}{3})}(k=0,1,2)\\[-19pt]\end{aligned}$
2. 原式 $\begin{aligned}=&\sqrt[3]{e^{i(-\frac{\pi}{2})}}\\=&e^{i(-\frac{\pi}{6}+\frac{2\pi k}{3})}(k=0,1,2)\\[-19pt]\end{aligned}$
3. 原式 $\begin{aligned}=&\sqrt[4]{e^{i\pi}}\\=&e^{i(\frac{\pi}{4}+\frac{\pi k}{2})}(k=0,1,2,3)\\[-19pt]\end{aligned}$

5. 证明题

由 $\omega^3=1$ 得 $(1-\omega)(1+\omega+\omega^2)=0$。
又由 $\omega$ 是复根，即 $\omega\not=1$ 得 $1+\omega+\omega^2=0$

6. 求 x, y

两边平方，$x^2-y^2+2xyi=a+ib$
$\therefore\begin{cases}x^2-y^2=a\\2xy=b\end{cases}$
$\therefore 4x^2y^2=b^2$
$\therefore 4x^2(x^2-a)=b^2$
解得 $\begin{cases}x^2=\frac{a+\sqrt{a^2+b^2}}{2}\\y^2=\frac{-a+\sqrt{a^2+b^2}}{2}\end{cases}$
根据实际情况，最终可得$\begin{cases}x=\pm\sqrt{\frac{a+\sqrt{a^2+b^2}}{2}}\\y=\pm\sqrt{\frac{-a+\sqrt{a^2+b^2}}{2}}\end{cases}$
其中 $b>0$ 时 $x,y$ 同号，$b<0$ 时 $x,y$ 异号

7. 证明等式

记 $\begin{aligned} z=&\sum\limits_{k=1}^n\cos k\theta+i\sin k\theta\\ =&e^{i\theta}\cdot\frac{1-e^{in\theta}}{1-e^{i\theta}}\\ =&\frac{(\cos\theta+i\sin\theta)(1-\cos\theta+i\sin\theta)(1-\cos n\theta-i\sin n\theta)}{2-2cos\theta}\\ =&\frac{\cos\theta-1+i\sin\theta}{2-2\cos\theta}\\[-78pt] \end{aligned}$

则有：$\begin{aligned} (1)=\operatorname{Re} z=&\frac{(\cos\theta-1)(1-\cos n\theta)+\sin\theta\sin n\theta}{2-2\cos\theta}\\ =&-\frac{1}{2}+\frac{(\cos\theta-1)\cos n\theta-\sin\theta\sin n\theta}{2\cos\theta-2}\\ =&-\frac{1}{2}+\frac{\cos(n+1)\theta-\cos n\theta}{2\cos\theta-2}\\ =&-\frac{1}{2}-\frac{2\sin(n+\frac{1}{2})\theta\sin\frac{1}{2}\theta}{2\cos\theta-2}\\ =&-\frac{1}{2}+\frac{2\sin(n+\frac{1}{2})\theta\sin\frac{1}{2}\theta}{2(2\sin^2\frac{1}{2}\theta)}\\ =&-\frac{1}{2}+\frac{\sin(n+\frac{1}{2})\theta}{2\sin\frac{1}{2}\theta}\\[-137pt] \end{aligned}$

以及：$\begin{aligned} (2)=\operatorname{Im} z=&\frac{(\cos\theta-1)(-\sin n\theta)+\sin\theta(1-\cos n\theta)}{2-2\cos\theta}\\ =&\frac{\sin n\theta+\sin\theta-\sin(n+1)\theta}{2-2\cos\theta}\\ =&\frac{(\sin n\theta-\sin(n+1)\theta)+\sin\theta}{2-2\cos\theta}\\ =&\frac{(-2\cos(n+\frac{1}{2}\theta)\sin\frac{1}{2}\theta)+2\sin\frac{1}{2}\theta\cos\frac{1}{2}\theta}{2(2\sin^2\frac{1}{2}\theta)}\\ =&\frac{1}{2}\cot\frac{\theta}{2}-\frac{\cos(n+\frac{1}{2})\theta}{2\sin\frac{1}{2}\theta}\\[-111pt] \end{aligned}$

8. 证明等式

设 $\arg\frac{z_1}{z_2}=\theta$ 则有
$\begin{cases} |z_1-z_2|^2=|z_1|^2+|z_2|^2-2|z_1||z_2|\cos\theta\\ |z_1+z_2|^2=|z_1|^2+|z_2|^2+2|z_1||z_2|\cos\theta \end{cases}$
两式相加得 $|z_1+z_2|^2+|z_1-z_2|^2=2(|z_1|^2+|z_2|^2)$
几何意义：

1. 平行四边形各边平方和等于对角线平方和
2. 三角形两边平方和的一半，等于对边中线的平方与对边的一半的平方的和

9. 求最大值

对任意复数 $t$ 满足 $|t|\le 1$, 若有 $z^n=t$，易知 $z$ 可取 $\sqrt[n]{|t|}e^{i\frac{1}{n}\arg t}$，且此时 $|z|\le 1$。

即：$z^n$ 可以组成所有模长 $\le 1$ 的复数的集合，即其方向任意且模长最大为 1

因此 $|z^n+a|_{\max}=|z^n|_{\max}+|a|=|a|+1$

最大值在 $z=e^{i\frac{1}{n}\arg t}$ 时取得

10. 证明

1. $\left|\frac{z-a}{1-\overline{a}z}\right|=\left|\frac{1-\frac{a}{z}}{1-\overline{a}z}\right|=\left|\frac{1-a\overline{z}}{1-\overline{a}z}\right|=\left|\frac{1-\overline{\overline{a}z}}{1-\overline{a}z}\right|=\left|\frac{\overline{1-\overline{a}z}}{1-\overline{a}z}\right|=1$

2. 原式直接平方，即证 $|z-a|^2<|1-\overline{a}z|^2$
   即证 $|z|^2+|a|^2-\overline{a}\cdot z-a\cdot\overline{z}<1+|\overline{a}z|^2-\overline{a}\cdot z-a\cdot\overline{z}$
   即证 $|z|^2+|a|^2<1+|\overline{a}z|^2$
   即证 $(|z|^2-1)(|a|^2-1)>0$
   在 $|z|<1,|a|<1$ 时显然

   ---

   如果使用 (1) 中式子，我们还有这样较为复杂的证明方法：
   首先设 $s=\frac{1}{|z|}$，显然 $s>1$。
   我们先证明不等式：$|k|>1,|v|<1$ 时 $|k-v|>|1-kv|$。
   证：两边平方，即证 $|k|^2+|v|^2-2|k|\cdot|v|>1+(|k|\cdot|v|)^2-2|k|\cdot|v|$
   即证 $|k|^2+|v|^2>1+(|k|\cdot|v|)^2$
   即证 $(|k|^2-1)(|v|^2-1)<0$
   在 $|k|>1,|v|<1$ 时显然成立

   代入：$k=s,v=sz\overline{a}$ 可得 $|s-sz\overline{a}|>|1-s^2z\overline{a}|$。
   可得 $\left|\frac{sz-sa}{s-sz\overline{a}}\right|<\left|\frac{sz-sa}{1-sz\cdot s\overline{a}}\right|=1$ （此处由 (1) 可得）
   上下同除以 $s$ 得 $\left|\frac{z-a}{1-z\overline{a}}\right|<1$
   证毕

11. 证明

1. 首先我们有 $|a|-|b|\le|a+b|\le|a|+|b|$，这是易证的，可以通过几何意义或者两端平方证得。反复运用此式，我们有：

   • $|z_2+z_3+\cdots+z_n|\le|z_2|+|z_3+\cdots+z_n|\le\cdots\le|z_2|+|z_3|+\cdots+|z_n|$
   • $|z_1+(z_2+z_3+\cdots+z_n)|\ge|z_1|-|z_2+z_3+\cdots+z_n|$

   因此可得 $|z_1+(z_2+z_3+\cdots+z_n)|\ge|z_1|-|z_2+z_3+\cdots+z_n|\ge|z_1|-|z_2|-|z_3|-\cdots-|z_n|$

2. 注意到 $|(1-z)P(z)|=|a_n+(a_{n-1}-a_{n})z+\cdots+(a_0-a_1)z^n-a_0z^{n+1}|$, 且有$a_{i+1}-a_{i}\geq0,i=0\cdots n-1$

   由第一问结论，原式 $\geq|a_n|-|(a_{n-1}-a_{n})z|-\cdots-|(a_0-a_1)z^n|-a_0|z|^{n+1}\geq a_n - (a_{n}-a_{n-1})-\cdots-(a_1-a_0)-a_0|z|^{n+1}=a_0(1-|z|^{n+1})>0$

   又 $|z|<1$, 故 $|z-1|>0$, 因此有 $|P(z)|>0$, 即 $P(z)=0$ 在 $|z|<1$ 内无根。

12. 证明：充分必要条件

我们只需证明 三点共线 ⇔ (3) ⇔ (1) ⇔ (2) 即可 （当然有别的做法，这只是一种证明路径）

证明：三点共线 ⇔ (3)

我们已知：对于向量 $v_1,v_2,v_3$，若三点共线，必有 $v_1=\lambda v_2+(1-\lambda)v_3(\lambda\in\mathbb{R})$。显然，对复数而言，本结论也成立。

不妨设 $\lambda_1\not=0$，那么 $z_1=-\frac{\lambda_2}{\lambda_1}z_2-\frac{\lambda_3}{\lambda_1}z_3$，且 $(-\frac{\lambda_2}{\lambda_1})+(-\frac{\lambda_3}{\lambda_1})=-\frac{\lambda_2+\lambda_3}{\lambda_1}=-\frac{-\lambda_1}{\lambda_1}=1$

因此 (3) $\Rightarrow$ 三点共线

又有：若三点共线，必有 $z_1=\lambda z_2+(1-\lambda)z_3(\lambda\in\mathbb{R})$。此时，取 $\lambda_1=-1,\lambda_2=\lambda,\lambda_3=1-\lambda$ 即可。

因此 三点共线 $\Rightarrow$ (3)

证明：(1) ⇔ (3)

设 $\frac{z_1-z_2}{z_2-z_3}=k$。那么可以取 $\lambda_1=1,\lambda_2=-k-1,\lambda_3=k$，显然符合 (3) 中条件，因此 (1) $\Rightarrow$ (3)。

若 $\lambda_1\not=0$，那么可得 $\frac{z_1-z_2}{z_2-z_3}=\frac{-\frac{\lambda_2z_2+\lambda_3z_3}{-(\lambda_2+\lambda_3)}-z_2}{z_2-z_3}=-\frac{\lambda_3}{\lambda_2+\lambda_3}$。
若 $\lambda_1=0,\lambda_2\not=0$，那么可得 $\lambda_2+\lambda_3=0$ 且 $\lambda_2z_2+\lambda_3z_3=0$，因此有 $z_2=z_3$，产生共点情况，排除。
显然不可能有 $\lambda_1=0,\lambda_2=0$ 的情况，因为若如此，必有 $\lambda_3=0$，矛盾。
因此 (3) $\Rightarrow$ (1)。

证明：(1) ⇔ (2)

设 $\frac{z_1-z_2}{z_2-z_3}=k$。
两边同时乘以 $\overline{z_2-z_3}$ 得到 $(z_1-z_2)(\overline{z_2}-\overline{z_3})=k|z_2-z_3|^2$。
展开移项得到 $z_1\overline{z_2}+z_2\overline{z_3}-z_1\overline{z_3}=k|z_2-z_3|^2+|z_2|^2$
因为 $\operatorname{Im}(-z_1\overline{z_3})=\operatorname{Im}(z_3\overline{z_1})$
所以 $z_1\overline{z_2}+z_2\overline{z_3}+z_3\overline{z_1}=k|z_2-z_3|^2+|z_2|^2+2\operatorname{Re}(z_3\overline{z_1})$

因此 (1) $\Rightarrow$ (2)

(2) $\Rightarrow$ (1) 同理易证，只需将这个过程反过来即可

13. 证明题

由 $z_1+z_2+z_3=0$ 得 $z_1+z_2=-z_3$，因此 $|z_1+z_2|=|-z_3|=1$。
利用余弦定理有 $|z_1|^2+|z_2|^2-2|z_1||z_2|\cos(180^\circ-\arg\frac{z_1}{z_2})=1^2$
因此 $\cos\arg\frac{z_1}{z_2}=\frac{1}{2}$，所以 $\arg\frac{z_1}{z_2}=\pm 120^\circ$
同理 $\arg\frac{z_1}{z_3}=\arg\frac{z_2}{z_3}=\pm 120^\circ$
唯一的可能是 $z_1,z_2,z_3$ 两两之间夹角均为 $120^\circ$，即 $z_1,z_2,z_3$ 构成了内接正三角形。显然该正三角形内接于单位圆。

14. 证明题

因为 $z_1+z_2$ 为实数，即 $(\operatorname{Re}z_1+\operatorname{Re}z_2)+i(\operatorname{Im}z_1+\operatorname{Im}z_2)$ 为实数，即 $\operatorname{Im}z_1+\operatorname{Im}z_2=0$
因为 $z_1z_2$ 为实数，即 $(\operatorname{Re}z_1\operatorname{Re}z_2-\operatorname{Im}z_1\operatorname{Im}z_2)+i(\operatorname{Re}z_1\operatorname{Im}z_2+\operatorname{Re}z_2\operatorname{Im}z_1)$ 为实数，即 $\operatorname{Re}z_1\operatorname{Im}z_2+\operatorname{Re}z_2\operatorname{Im}z_1=0$。由 $\operatorname{Im}z_1+\operatorname{Im}z_2=0$ 易知 $\operatorname{Re}z_1=\operatorname{Re}z_2$。

综上所述，显然有 $z_1=\overline{z_2}$，即 $z_1$ 与 $z_2$ 或者都为实数，或者为一对共轭复数。

15. 求另二顶点

当 $a,b$ 是俩相邻顶点：考虑可以用 $i(b-a)$ 构造出正方形的垂直于 $b-a$ 的边，因此答案为 $a+i(b-a), b+i(b-a)$ 或者 $a+i(a-b), b+i(a-b)$

当 $a,b$ 为俩对角顶点：仍然考虑另一条对角线的构造（应为 $i(b-a)$），并用 $a,b$ 的中点定位求出另俩个顶点，答案为 $\frac{a+b}{2}+i\frac{b-a}{2},\frac{a+b}{2}+i\frac{a-b}{2}$（另解：可以仍从 $a$ 点出发，利用 $\frac{1}{\sqrt{2}}e^{\frac{\pi}{4}i}$ 对对角线作旋转与缩放得到另外的节点。此方法的答案为 $a+\frac{b-a}{\sqrt{2}}e^{\frac{\pi}{4}i},a+\frac{b-a}{\sqrt{2}}e^{-\frac{\pi}{4}i}$）

共 3 个答案

16. 复数列求极限

请注意：下方并非由模长极限为 0 得出数列极限为 0（没有该定理），实际上是由 $\lim\limits_{n\rightarrow+\infty}|z_n-0|=0$ 得出数列极限为0

1. 通项：$z_n=\left(\frac{3+4i}{6}\right)^n$
   模长通项：$|z_n|=\left(\frac{5}{6}\right)^n$
   模长极限：$\lim\limits_{n\rightarrow+\infty}|z_n|=0$
   因此原式有极限，极限为 $\lim\limits_{n\rightarrow+\infty}z_n=0$
2. 通项：$z_n=\frac{i^{n-1}}{n}$
   模长通项：$|z_n|=\frac{1}{n}$
   模长极限：$\lim\limits_{n\rightarrow+\infty}|z_n|=0$
   因此原式有极限，极限为 $\lim\limits_{n\rightarrow+\infty}z_n=0$
3. 通项：$z_n=i^{n-1}$，且有性质 $|z_{x+1}-z_x|=\sqrt{2}(x=1,2,\cdots)$
   若复数列有极限 $z_0$，不妨设 $n>N$ 时 $|z_n-z_0|<\frac{1}{2}$。那么我们有 $\sqrt{2}=|z_{n+2}-z_{n+1}|\le|z_{n+2}-z_0|+|z_{n+1}-z_0|<1$，从而导出矛盾，故该复数列无极限

17. 证明题

1. 对任意 $\varepsilon>0$，有一个 $N$ 使 $n>N$ 时 $|z_n-z_0|<\varepsilon$。取 $N^\prime=N$，则 $n>N^\prime$ 时 $|\overline{z_n}-\overline{z_0}|=|\overline{z_n-z_0}|=|z_n-z_0|<\varepsilon$，从而 $\overline{z_n}\rightarrow\overline{z_0}$

2. 当 $z_0$ 不为 0 或者负数时，对任意 $0<\varepsilon<\pi-|\arg z_0|$，取 $\delta=|z_0|\sin\varepsilon$，则存在 $N$ 使 $n>N$ 时 $|z_n-z_0|<\delta$。注意到 $|\arg z_n-\arg z_0|\le\arcsin\frac{|z_n-z_0|}{|z_0|}$（在 $z_n,z_0$ 没有分居 $y$ 轴负半轴两侧时），因此 $|\arg z_n-\arg z_0|<\varepsilon$。故：$\arg z_n\rightarrow\arg z_0$

   当 $z_0=0$ 时 $\arg z_0$ 无意义
   当 $z_0$ 为负数时不一定有 $\arg z_n\rightarrow\arg z_0$。反例：$z_n=e^{-i\pi\cdot(\frac{n-1}{n})}$，$z_0=-1$，$\arg z_n\rightarrow-\pi$，$\arg z_0=\pi$

3. 对于 (1) 中结论，仍然成立
   对于 (2) 中结论，$\arg\infty$ 无意义，结论的成立与否无意义

18. 曲线作图题

本题仅给出图像，计算过程略
第 3,4,5 题误删了坐标轴，图像仅供参考

1. 由距离相等，易知是点 $a,b$ 连线的中垂线
2. 是椭圆的一种定义，为焦点是 $a,b$ 的椭圆
3. 与 y 轴相切于原点的圆族及 y 轴（$\alpha=0$ 时）
   请注意：图像在原点不连续
   
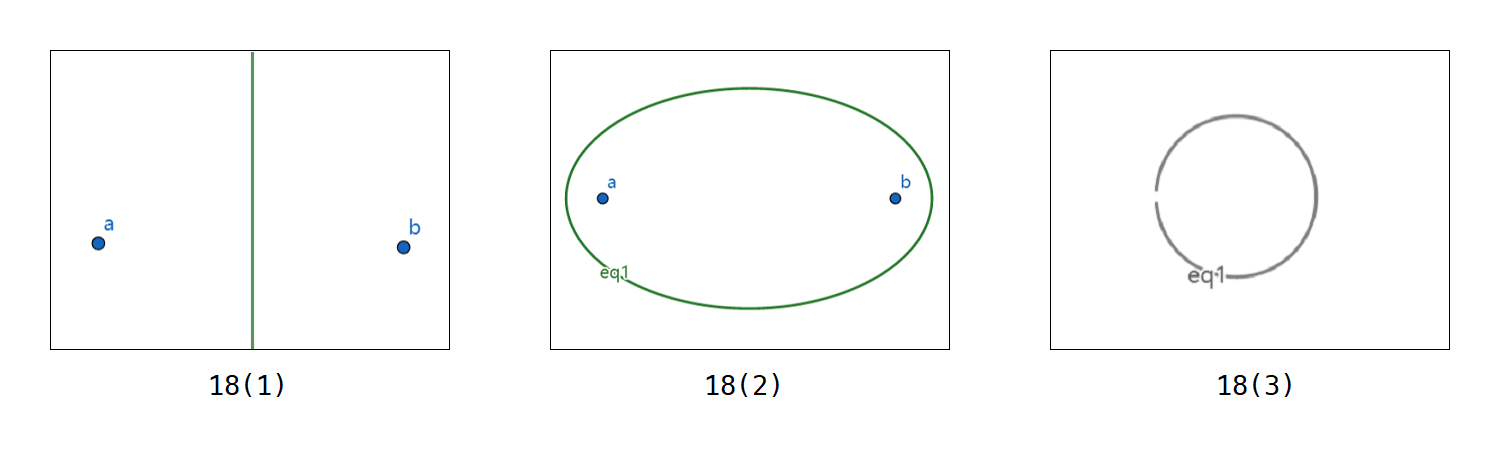
4. 经过点 $(\pm1,0)$ 的圆族及 x 轴（$\alpha=0$ 时）
   （可以形象为：两个钉子，一把三角尺卡住移动（旋转），直观感受为圆形）
5. 以点 $(\pm1,0)$ 为对称点的圆族及 y 轴（$\alpha=1$ 时）
   （对称的 Apollonius 圆族）

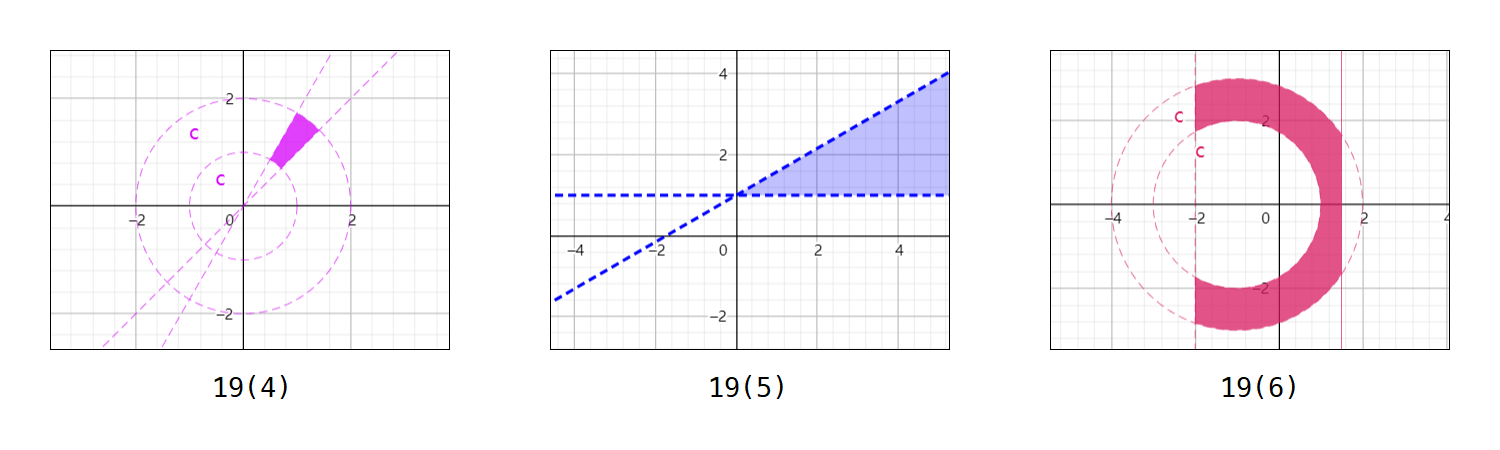
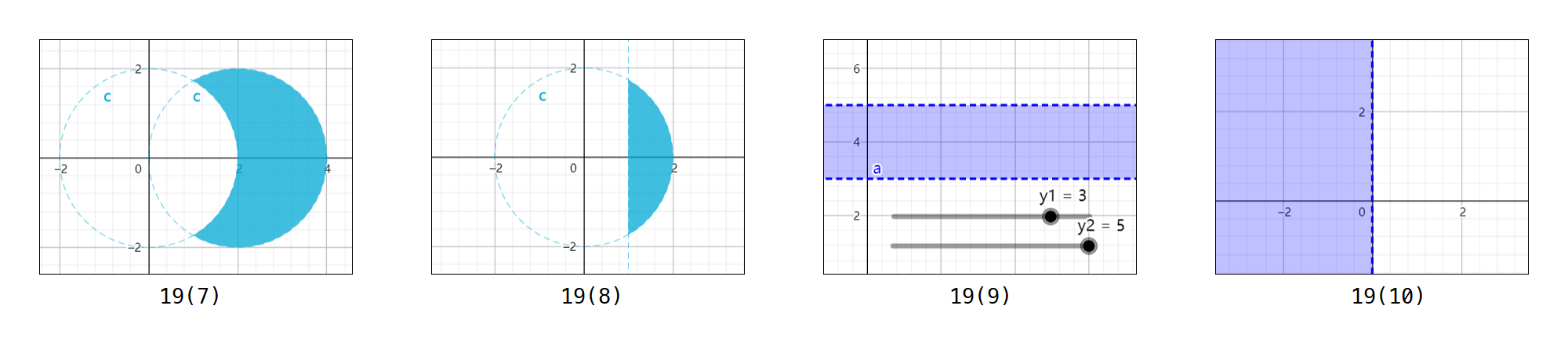
19. 画出点集图像

本题略去过程，仅阐述结论

1. 是区域；边界为 $\{P\mid x_P=2\}$
2. 不是区域；边界为 $\{P\mid y_P=3\}$
3. 是区域；边界为 $\{P\mid x_P=y_P\vee x_P=-y_P,x_P\ge0\}$
4. 是区域；边界为 $\{P\mid r_P=1\vee r_P=2,\frac{\pi}{4}<\theta_P<\frac{\pi}{3}\}\cup\{P\mid y_P=x_P,\frac{\sqrt{2}}{2}\le x_P\le\sqrt{2}\}\cup\{P\mid y_P=\sqrt{3}x_P,\frac{1}{2}\le x_P\le1\}$
5. 是区域；边界为 $\{P\mid y_P=1\vee y_P=\frac{1}{2}x_P+1,x_P\ge0\}$
6. 不是区域；边界为 $\{P\mid x_P=-2,\sqrt{3}\le |y_P|\le2\sqrt{2}\}\cup\{P\mid x_P=\frac{3}{2},|y_P|\le\frac{\sqrt{11}}{2}\}\cup\{P\mid r_P=2\vee r_P=3,-2\le x_P\le\frac{3}{2}\}$
7. 是区域；边界为 $\{P\mid r_P=2\vee\sqrt{(x-2)^2+y^2}=2,x_P\ge1\}$
8. 是区域；边界为 $\{P\mid r_P=2,x_P\ge1\}\cup\{P\mid x_P=1,|y_P|\le\sqrt{3}\}$
9. 不是区域；边界为 $\{P\mid y_P=y_1\vee y_P=y_2\}$
10. 是区域；边界为 $\{P\mid x_P=0\}$

20. 证明题

因为任意直线可以视为一条垂直平分线，即存在复数$a,b$，使直线方程为$\frac{|z-a|}{|z-b|}=1$，两边平方化简得：$(\bar a -\bar b)z+(a-b)\bar z=|a|^2-|b|^2$，再令$\bar a -\bar b=\alpha,c=|a|^2-|b|^2$ 即得证

21. 求曲线

可以看成 $x=\operatorname{Re} z,y=\operatorname{Im} z$ 的参数方程来求解

1. $x=t,y=t,-\infty<t<+\infty$ 因此曲线为 $y=x$，一根经过原点的直线
2. $x=a\cos t,y=b\sin t,0\le t\le 2\pi$ 因此曲线为 $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$，是以 $(0,0)$ 为中心，$a,b$ 分别为半长轴与半短轴的椭圆
3. $x=t,y=\frac{1}{t},t\not=0$ 因此曲线为 $y=\frac{1}{x}$，双曲线
4. $x=t^2,y=\frac{1}{t^2},t>0$ 因此曲线为 $y=\frac{1}{x}$ 的 $x>0$ 部分，为双曲线的一支

22. 证明题

带入 $x=(z+\bar z)/2,y=(z-\bar z)/2$，原式可化为：

$(z +1)^2+(\bar z +1)^2=4$

注意到 $x^2+\bar x^2=2((\operatorname{Re} x)^2+(\operatorname{Im} x)^2)=2|x|^2$

所以 $2|z+1|^2=4$

简化可得 $|z+1|=\sqrt{2}$